Hemos visto la semana pasada cómo, efectivamente, las preferencias estéticas pueden influir sobre los descubrimientos científicos. Hemos visto que a pesar de que Galileo y Harriot observaron la misma Luna, con instrumentos y conocimientos científicos más o menos similares y en la misma época, no interpretaron sus observaciones de la misma manera. Uno podría argumentar que el problema consistió en una cuestión de percepción; que la observación de un fenómeno introduce una cierta dosis de subjetividad y que por lo tanto estos «errores» no podrían ocurrir en disciplinas más abstractas, como por ejemplo las matemáticas. Y entonces uno volvería a equivocarse porque el problema es mucho más profundo que el simple hecho de observar a través de un telescopio. Se trata de cómo miramos el mundo, de qué carga estética o teórica condiciona nuestra visión del mundo. Veremos en este post cómo los prejuicios estéticos pueden también condicionar los descubrimientos matemáticos.
El imperdonable error de Giovanni Girolamo Saccheri
En este ejemplo veremos cómo un (casi) desconocido matemático podría haber pasado a la historia como el fundador de la geometría no-euclideana de no haberse dejado llevar por sus prejuicios estéticos acerca de la naturaleza de la línea recta. Echemos entonces una rápida mirada a quién era Saccheri y veamos por qué no figura en los libros grandes de matemática. Giovanni Girolamo Saccheri nació en 1667 en San Remo, Italia. Siendo aun muy joven ingresó en la orden de la Compañía de Jesús y en 1690 fue enviado a Milán para estudiar gramática y enseñar filosofía y teología. Allí se inició en las matemáticas y tomó contacto con los Elementos de Euclides. La geometría euclideana está asentada en cinco postulados que Euclides consideró como verdades evidentes. Hoy sabemos que los postulados constituyen el punto de partida de cualquier sistema formal pero que no necesariamente constituyen verdades evidentes (ni siquiera verdades a secas). Los primeros cuatro postulados de la geometría euclideana pueden ser aceptados sin demasiados remordimientos. Sin embargo, el quinto postulado (conocido como el postulado de las paralelas [i]) es un tanto difícil de digerir y durante siglos muchos matemáticos han intentado (infructuosamente) derivarlo a partir de los otros cuatro. Saccheri se sintió enseguida atraído por el postulado de las paralelas y dedicó el resto de su vida a demostrar la consistencia de la geometría euclideana.
Saccheri abordó el problema desde una nueva perspectiva: la reducción al absurdo. Supuso que el quinto postulado era falso y comenzó a derivar a partir de allí nuevos teoremas. Según su punto de vista (eufemismo de prejuicio) no tardarían en aparecer contradicciones que mostrarían categóricamente que si la negación del quinto postulado es falsa entonces el quinto postulado es verdadero. Saccheri derivó durante años teorema tras teorema sin encontrar la más mínima contradicción. Sin embargo, los nuevos teoremas (todos verdaderos una vez aceptados los axiomas) lo estaban llevando a conclusiones que él consideraba, textualmente, repugnantes a la naturaleza de la línea recta. Este hecho constituiría para él la prueba irrefutable de la contradicción que había estado buscando durante años. Saccheri interpretó erróneamente un criterio estético como una prueba matemática irrefutable. En 1733 publicó sus hallazgos en un libro titulado “Euclides. Ab omni naevo vindicatus” que vendría a ser algo así como “Euclides librado de toda imperfección”… y murió. No había en sus resultados nada matemáticamente incorrecto, el problema fue que éstos eran incompatibles con los criterios estéticos del momento y su apego a las ideas euclideanas no le permitieron ver la magnitud y relevancia de sus hallazgos.
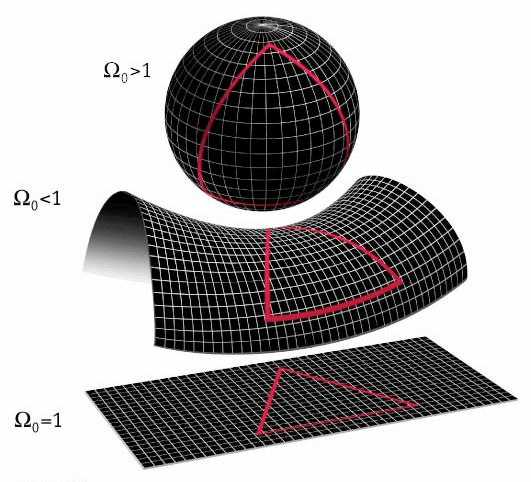
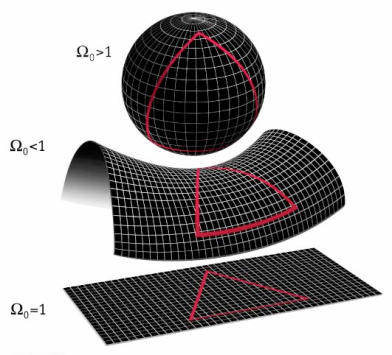
A principios del Siglo XIX, de manera independiente y simultánea, y sin conocer el trabajo de Saccheri, János Bolyai, Carl Friedrich Gauss, Ferdinand Schweickard y Nikolai Lobachevsky descubren la geometría hiperbólica (no-euclideana) a partir de negar el quinto postulado de Euclides. Sacchieri podría haber sido el gran adelantado, el gran fundador de las geometrías no-euclideanas; pero no fue capaz de aceptar la idea de espacios curvos. La sola posibilidad de tales espacios le parecía literalmente repugnante. Sacchieri estaba atrapado en un paradigma estético y cultural y no supo salirse. No sólo pagó un alto precio, sino que la sociedad en su conjunto vio retrasado en casi un siglo el desarrollo de ciertas ideas estéticas y matemáticas. ¿Cuántas cosas nos estaremos perdiendo por no ser capaces de salirnos del paradigma dominante?
En el próximo (y último) post de esta serie veremos que hasta un tal Albert Einstein fue víctima de los prejuicios estéticos.
[i] En su versión más conocida, el quinto postulado dice que: “por un punto exterior a una recta pasa una y sólo una recta paralela a la primera”. Una versión equivalente consiste en postular que: “los ángulos interiores de un triángulo suman 180º”.

Me ha gustado mucho esta entrada. En reallidad me gusta todo el blog, pero esta entrada me ha gustado especialmente. Quizás por mi debilidad por las geometrías no euclídeas y por cómo parece que la realidad última está muy apartada de nuestra representación espacial habitual euclídea, que es parece la más intuitiva. Es un engaño de nuestros sentidos o de nuestras categorías mentales? De esto han hablado varios filósofos a lo largo de la historia y no me voy a extender. Simplemente pondré un ejemplo que ilustra la idea de que incluso las matemáticas, ese edificio que se erige por la propia lógica de las proposiciones y que no estaría contaminado por nuestros sentidos o sesgos mentales, también se ve seriamente influenciado por la imagen misma con la que nos representamos una simple operación aritmética. Los antiguos griegos no tenían los conceptos de cero y números negativos. Y esto era así por dos razones. Primero, por su idea del ser y de que no cabe que lo que es no sea, ni que lo que no es, sea. Esto tiene su expresión en el «horror vacui» en la física de Aristoteles, como principio explicativo evidente, o en el hecho de que no tenían el cero, no sabían contar nada. Segundo porque la imagen rectora de la resta de dos números era la de extracción o substracción (y así se sigue enseñando). La operación 4-7 sería absurda. Si tengo cuatro ovejas, puedo quitar una, dos, tres, cuatro… Y ahí ya me quedo sin nada. ¿Cómo voy a poder quitar 3 más? De donde no hay no puede ya extraerse nada (volvemos a la primera razón de nuevo). Sin embargo, si sustituimos la imagen rectora de la resta por otra, por ejemplo por la de oposición o enfrentamiento (como concebían los chinos la resta) entonces la cosa cambia mucho y la operación 4-7 es una tontería: puedo enfrentar mis 4 ovejas a tus 7 ovejas y el resultado de esta operación es que tengo tres menos que tú. No hay problema para asumir los números negativos, no son una mera ficción de la mente. Los chinos que dividen todo en dos mitades, que representan la realidad del ser polarizada (el famoso yin y yang) nunca han tenido problemas con que los números negativos sean tan naturales como los positivos. De esta forma, podemos pensar que incluso el maravilloso e impoluto mundo de las matemáticas, el colmo de la objetividad y universalidad, está contaminado por estructuras mentales pre-lógicas, ya sean estéticas (como tú estás exponiendo) o intelectuales-ideológicas…
Todo esto da para una buena conversación, ¿no crees?
Gracias Igor por tu comentario y tu ejemplo sobre los números negativos. Si no fuera porque nos conocemos, diría que me estas plagiando entradas viejas del blog. No sólo estoy absolutamente de acuerdo con lo que dices, sino que he usado casi las mismas palabras que tú para decir lo mismo. Mira, por ejemplo, las entradas https://gustavoarielschwartz.org/2012/06/ acerca del horror vacui o esta https://gustavoarielschwartz.org/2012/06/ acerca de la resta en china. Hay un libro de Emmanuel Lizcano Fernández que se titula «Metáforas que nos piensan» que me encanta y habla sobre todas estas cosas. Es realmente sorprendente cómo una determinada cosmovisión del mundo condiciona nuestra manera de pensar (incluso la matemática). Ya tendremos ocasión de conversar extensamente todo esto. Un abrazo, G/
Gustavo
Lei el texto que mencionas de Lizcano hace ya mucho tiempo y me impacto muchísimo y cambió mi idea de las matemáticas. De hecho lo que te cuento en el comentario es lo que recuerdo. Se me quedo grabado el tema de la resta, aunque el hablaba de más cosas. Lo voy a recuperar y lo releeré para ir preparado a la conversación.
Acepto el coscorrón de no haber leído las entradas que mencionas. No ha habido plagio, te lo aseguro, porque no las conocía. Me quedo con lo que suele decir Pedro de «Great minds think alike»… Aunque ya conocerás también la segunda parte de la frase, que esa sí, la dejo para la conversación.
Un abrazo
Igor
Ahora entiendo por qué tu comentario y mis entradas anteriores son tan parecidos (lo del plagio era broma, obviamente); ambos leímos el libro de Lizcano (mis entradas están basadas en el libro). Te cuento de paso que Emmanuel fue parte del comité académico del encuentro de Mestizajes en 2011 y tuve la suerte de poder charlar con él, café de por medio, durante media mañana. Es un tipo muy interesante y que sabe mogollón de cosas sobre epistemología de las matemáticas. Un abrazo, G/
Pingback: Cuerdos De Atar
Pingback: Las preferencias estéticas y los descubrimientos científicos (III) – Arte, Literatura y Ciencia
Pingback: Los límites de la imaginación – Arte, Literatura y Ciencia